如图,在平面直角坐标系中,直线l: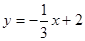 交y轴于点A.抛物线
交y轴于点A.抛物线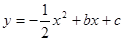 的图象过点E(-1,0),并与直线l相交于A、B两点.
的图象过点E(-1,0),并与直线l相交于A、B两点.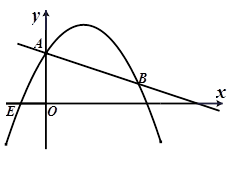
⑴ 求抛物线的解析式;
⑵ 设点P是抛物线的对称轴上的一个动点,当△PAE的周长最小时,求点P的坐标;
⑶ 在x轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
根据右图拼图的启示:
(1)计算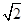 +
+ =________;
=________;
(2)计算 +
+ =________;
=________;
(3)计算 +
+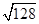 =________.
=________.
把下列各数分别填在相应的集合中:
- ,
, ,-
,-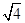 ,0,-
,0,-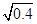 ,
, 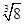 .
. ,
,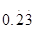 ,3.14
,3.14
已知函数y1=kx-2和y2=-3x+b相交于点A(2,-1)
(1)求k、b的值,在同一坐标系中画出两个函数的图象.
(2)利用图象求出:当x取何值时有:①y1<y2;②y1≥y2
(3)利用图象求出:当x取何值时有:①y1<0且y2<0;②y1>0且y2<0
在同一坐标系中画出一次函数y1=-x+1与y2=2x-2的图象,并根据图象回答下列问题:
(1)写出直线y1=-x+1与y2=2x-2的交点P的坐标.
(2)直接写出:当x取何值时y1>y2;y1<y2
某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶xkm,应付给个体车主的月租费是y元,付给出租车公司的月租费是y元,y,y分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题: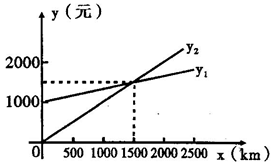
(1)每月行驶的路程在什么范围内时,租国有出租车公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?