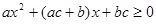(本小题满分12分)设圆C: ,此圆与抛物线
,此圆与抛物线
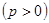 有四个不同的交点,若在
有四个不同的交点,若在 轴上方的两交点分别为
轴上方的两交点分别为 ,
,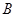 ,坐标原点为
,坐标原点为 ,
,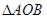 的面积为
的面积为 。
。
(1)求实数 的取值范围;
的取值范围;
(2)求 关于
关于 的函数
的函数 的表达式及
的表达式及 的取值范围。
的取值范围。
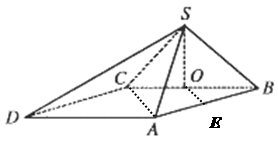
(本小题满分13分)四棱锥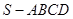 中,底面
中,底面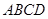 为平行四边形,且
为平行四边形,且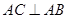 ,
,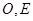 分别为
分别为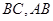 的中点.已知
的中点.已知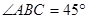 ,
,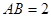 ,
,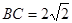 ,
,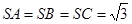 ,
,
(1)求证:平面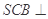 平面
平面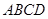 ;
;
(2)求三棱锥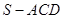 的体积;
的体积;
(3)求二面角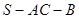 的大小.
的大小.
某企业生产A,B两种产品,生产每一吨产品所需的劳动力、煤和电耗如下表:
| 产品品种 |
劳动力(个) |
煤(吨) |
电(千瓦) |
| A产品 |
3 |
9 |
4 |
| B产品 |
10 |
4 |
5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业如何安排生产,才能获得最大利润?
(本小题满分12分)已知向量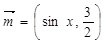 ,
,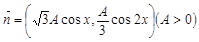 ,
,
函数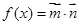 的最大值为6.
的最大值为6.
(1)求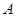 ;
;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求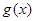 在
在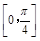 上的值域.
上的值域.
(本小题满分12分)已知圆C经过点 ,和直线
,和直线 相切,且圆心在直线
相切,且圆心在直线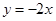 上.
上.
(1)求圆C的方程;
(2)已知直线l经过原点,并且被圆C截得的弦长为2,求直线l的方程.
(本小题满分12分)已知关于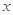 的不等式
的不等式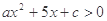 的解集为
的解集为 ,
,
(1)求 的值;
的值;
(2)解不关于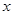 的不等式
的不等式