(14分）如图所示，高为0.3m的水平通道内，有一个与之等高的质量为M＝1.2kg表面光滑的立方体，长为L＝0.2m的轻杆下端用铰链连接于O点，O点固定在水平地面上竖直挡板的底部（挡板的宽度可忽略），轻杆的上端连着质量为m＝0.3kg的小球，小球靠在立方体左侧。取g＝10m/s2，sin37°＝0.6，cos37°＝0.8。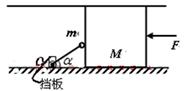
（1）为了使轻杆与水平地面夹角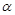
＝37°时立方体平衡且不动，作用在立方体上的水平推力F1应为多大？
（2）若立方体在F2＝4.5N的水平推力作用下从上述位置由静止开始向左运动，则刚要与挡板相碰时其速度多大？
（3）立方体碰到挡板后即停止运动，而轻杆带着小球向左倒下碰地后反弹恰好能回到竖直位置，若小球与地面接触的时间为t＝0.05s，则小球对地面的平均冲击力为多大？
（4）当杆回到竖直位置时撤去F2，杆将靠在立方体左侧渐渐向右倒下，最终立方体在通道内的运动速度多大？
如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接。现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点。已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m。（滑块经过B点时没有能量损失，g=10m/s2），求：
（1）滑块在运动过程中的最大速度；
（2）滑块与水平面间的动摩擦因数μ；
（3）滑块从A点释放后，经过时间t=1.0s时速度的大小。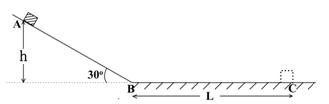
某课外小组经长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R1，周期为T1，已知万有引力常为G。求：
⑴行星的质量；
⑵若行星的半径为R，行星的第一宇宙速度；
⑶通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R2，周期为T2，试估算靠近行星周围众多卫星的总质量。
如图所示，半径为R，内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点c时，对管上部的压力为3mg，b通过最高点c时，对管下部的压力为0．75mg。求a,b两球落地点间的距离。
为了研究太阳演化进程，需知道目前太阳的质量M。已知地球半径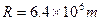
，地球质量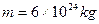
，日地中心距离
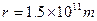，地球表面处的重力加速度
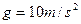，地球绕太阳一周所用的时间1年约为
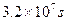，试估算目前太阳的质量M（保留一位有效数字，引力常量未知）
如图，在一圆柱形筒中有一小物体恰能靠在筒壁上随筒一起匀速转动，已知小物体与筒壁间的最大静摩擦力等于正压力的1/4，小物体中心到转轴的距离r=0．3m,求筒转动的角速度ω。（g取10m/s2）