一个袋中装有大小相同的黑球、白球和红球. 已知袋中共有10个球,从中任意摸出1个球,得到黑球的概率是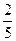 ,从中任意摸出2个球,至少得到1 个白球的概率是
,从中任意摸出2个球,至少得到1 个白球的概率是 . 求:
. 求:
(1)从中任意摸出2个球,得到的都是黑球的概率;
(2)袋中白球的个数
(本小题12分)
已知某商品的价格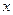 (元)与需求量
(元)与需求量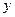 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
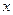 |
14 |
16 |
18 |
20 |
22 |
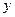 |
12 |
10 |
7 |
5 |
3 |
(1)画出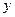 关于
关于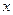 的散点图
的散点图
(2)用最小二乘法求出回归直线方程
(3)计算 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。
.(本小题12分)已知函数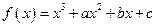 ,在曲线
,在曲线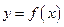 上的点
上的点 处的切线方程是
处的切线方程是 ,且函数在
,且函数在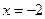 处有极值。
处有极值。
(1)求 的解析式
的解析式
(2)求 在
在 上的最值
上的最值
(本小题12分)
若 ,证明
,证明
 (本小题12分)
(本小题12分)
若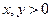 且
且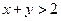 ,求证
,求证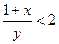 和
和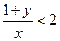 中至少有一个成立。
中至少有一个成立。