调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表:利用2×2列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?
| |
采桑 |
不采桑 |
合计 |
| 患者人数 |
18 |
12 |
|
| 健康人数 |
5 |
78 |
|
| 合计 |
|
|
|
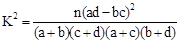
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
等比数列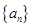 中,
中,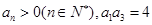 ,且
,且 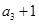 是
是 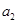 和
和 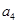 的等差中项,若
的等差中项,若 
(Ⅰ)求数列 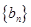 的通项公式;
的通项公式;
(Ⅱ)若数列 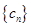 满足
满足  ,求数列
,求数列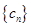 的前n项和
的前n项和
已知 ABC外接圆O的半径为1,且
ABC外接圆O的半径为1,且 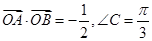 ,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为
,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为 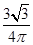 ,则
,则 MBC的形状为
MBC的形状为
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
已知函数 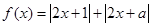
(Ⅰ)a=-3时,求不等式  的解集;
的解集;
(Ⅱ)若关于x的不等式 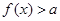 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
在直角坐标系中,以原点为极点,x轴的正半辐为极轴建立极坐标系,已知曲线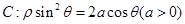 ,过点P(-2,-4)的直线
,过点P(-2,-4)的直线 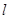 的参数方程为:
的参数方程为: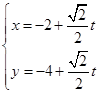 (t为参数),直线
(t为参数),直线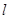 与曲线C相交于M,N两点.
与曲线C相交于M,N两点.
(Ⅰ)写出曲线C的直角坐标方程和直线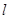 的普通方程;
的普通方程;
(Ⅱ)若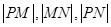 成等比数列,求a的值
成等比数列,求a的值
如图,四边形ABCD是边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的半圆O交于点C、F,连接CF并延长交AB于点E.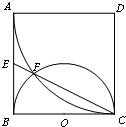
(Ⅰ)求证:E是AB的中点。
(Ⅱ)求线段BF的长.