(本小题满分13分)如图,9个正数排列成3行3列,其中每一行的数成等差数列,每一列的数成等比数列,且所有的公比都是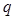 ,已知
,已知 ,
, 又设第一行数列的公差为
又设第一行数列的公差为 .
.
(Ⅰ)求出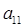 ,
, 及
及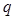 ;
;
(Ⅱ)若保持这9个数的位置不动,按照上述规律,补成一个n行n列的数表如下,试写出数表第n行第n列 的表达式,并求
的表达式,并求 的值.
的值.
已知函数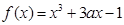 ,
,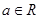 .
. (Ⅰ)若函数
(Ⅰ)若函数 的图象在
的图象在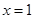 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数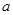 的值;
的值;
(Ⅱ)设函数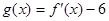 ,对满足
,对满足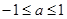 的一切
的一切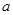 的值,都有
的值,都有 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)当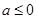 时,请问:是否存在整数
时,请问:是否存在整数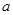 的值,使方程
的值,使方程 有且只有一个实根?若存在,求出整数
有且只有一个实根?若存在,求出整数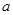 的值;否则,请说明理由.
的值;否则,请说明理由.
已知数列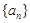 和
和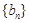 中,数列
中,数列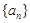 的前
的前 项和记为
项和记为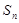 . 若点
. 若点 在函数
在函数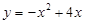 的图象上,点
的图象上,点 在函数
在函数 的图象上.
的图象上.
(Ⅰ)求数列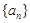 的通项公式;
的通项公式;
(Ⅱ)求数列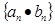 的前
的前 项和
项和
已知定义域为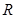 的函数
的函数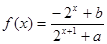 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的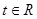 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围
在△ABC中,角A、B、C所对的边分别是a、b、c,tanA=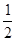 ,cosB=
,cosB= .
.
(Ⅰ)求角C;
(Ⅱ)若△ABC的最短边长是 ,求最长边的长.
,求最长边的长.
(Ⅰ)已知| |=4,|
|=4,| |=3,(2
|=3,(2 -3
-3 )·(2
)·(2 +
+ )=61,求
)=61,求 与
与 的夹角θ;
的夹角θ;
(Ⅱ)设 =(2,5),
=(2,5), =(3,1),
=(3,1),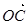 =(6,3),在
=(6,3),在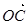 上是否存在点M,使
上是否存在点M,使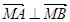 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.