已知A={x|x2≥9},B={x| ≤0},C={x||x-2|<4}.
≤0},C={x||x-2|<4}.
(1)求A∩B及A∪C;
(2)若U=R,求A∩∁U(B∩C)
(本小题满分10分)从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题.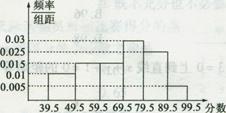
(I)在79.5~89.5之间的频率、频数分别是多少?
(Ⅱ)估计这次环保知识竞赛的及格率(60分及以上为及格).
(本小题满分10分)如图,过抛物线 上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点
上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点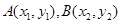
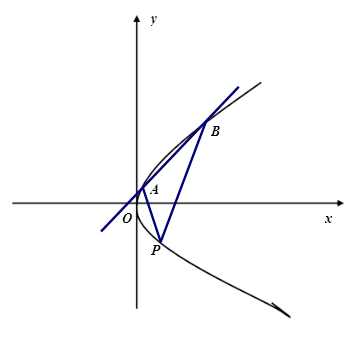
(1)求 的值;
的值;
(2)若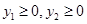 ,求
,求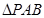 面积的最大值。
面积的最大值。
(本小题满分10分)如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)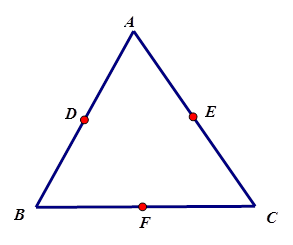
(1)求 ;
;
(2)求E(X)
选修4-5:不等式选讲(本小题满分10分)已知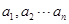 都是正数,且
都是正数,且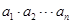 =1,求证:
=1,求证: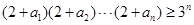
选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线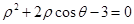 上的动点,B为直线
上的动点,B为直线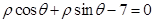 上的动点,求AB的最小值。
上的动点,求AB的最小值。