已知:某矩形的两条对角线所在直线的方程分别为l1:x+1=0,l2:3x-4y+15=0,它的较短边长为 ,求:(1)两条对角线的夹角大小;(2)各边所在直线的方程。
,求:(1)两条对角线的夹角大小;(2)各边所在直线的方程。
已知命题 :关于
:关于 的不等式
的不等式 <
< 无解;命题
无解;命题 :函数
:函数 =
= 的值域为R.若“
的值域为R.若“ 或
或 ”为真,“
”为真,“ 且
且 为假”,求实数
为假”,求实数 的取值范围.
的取值范围.
已知数列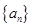 是首项为
是首项为 ,公比为
,公比为 的等比数列,设
的等比数列,设 ,数列
,数列 满足
满足 .
.
(1)求证: 是等差数列;
是等差数列;
(2)求数列 的前
的前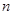 项和
项和 ;
;
(3)若 对一切正整数
对一切正整数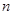 恒成立,求实数
恒成立,求实数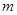 的取值范围.
的取值范围.
已知函数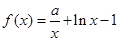 (a是常数,
(a是常数, ).
).
(1)求函数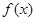 的极值;
的极值;
(2)当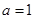 时,方程
时,方程 在
在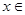
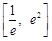 上有两解,求实数
上有两解,求实数 的取值范围.
的取值范围.
单调递增数列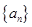 的前
的前 项和为
项和为 ,满足
,满足 .
.
(1)求 ,
, ,并求数列
,并求数列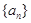 的通项公式;
的通项公式;
(2)设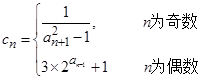 ,求数列
,求数列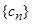 的前
的前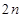 项和
项和 .
.
某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组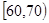 ,第二组
,第二组 ,……,第八组
,……,第八组 ,下图是按上述分组方法得到的频率分布直方图的一部分.
,下图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)估计该校的2000名学生这次考试成绩的平均分(可用中值代替各组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取两名,求他们的分差不小于10分的概率.