已知抛物线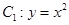 ,
,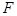 为抛物线的焦点,椭圆
为抛物线的焦点,椭圆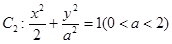 ;
;
(1)若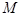 是
是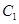 与
与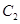 在第一象限的交点,且
在第一象限的交点,且 ,求实数
,求实数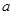 的值;
的值;
(2)设直线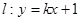 与抛物线
与抛物线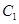 交于
交于 两个不同的点,
两个不同的点, 与椭圆
与椭圆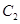 交于
交于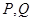 两个
两个
不同点,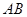 中点为
中点为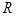 ,
, 中点为
中点为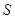 ,若
,若 在以
在以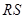 为直径的圆上,且
为直径的圆上,且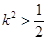 ,求实数
,求实数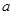
的取值范围.
已知函数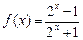 ,
,
(1)判断函数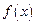 的奇偶性;
的奇偶性;
(2)求证: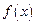 在
在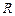 上为增函数;
上为增函数;
(3)求证:方程 至少有一根在区间
至少有一根在区间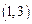 .
.
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业.分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(0<x<100).而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元.
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
已知函数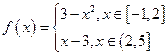 ,(1)在如图给定的直角坐标系内画出
,(1)在如图给定的直角坐标系内画出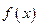 的图象;(2)写出
的图象;(2)写出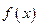 的单调递增区间.
的单调递增区间.
若集合A={x|x2-3x+2=0}, B={x|x2-mx+1=0}, A∩B=B,求实数m的取值范围.
(本小题满分12分)已知函数 的定义域为R,对任意的
的定义域为R,对任意的 都满足。
都满足。
(I)判断 的单调性和奇偶性;
的单调性和奇偶性;
(II)是否存在这样的实数m,当 时,不等式
时,不等式
对所有 恒成立,如存在,求出m的取值范围;若不存在,说明理由。
恒成立,如存在,求出m的取值范围;若不存在,说明理由。