如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5。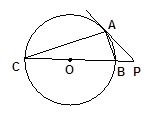
求:(1)⊙O的半径;
(2)s1n∠BAP的值。
已知椭圆C: 的离心率为
的离心率为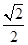 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线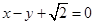 相切。
相切。
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C交于两点A和B,设P为椭圆上一点,且满足
 ·
· (O为坐标原点),当
(O为坐标原点),当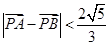 时,求实数t取值范围。
时,求实数t取值范围。
为迎接2013年“两会”(全国人大3月5日-3月18日、全国政协3月3日-3月14日)的胜利召开,某机构举办猜奖活动,参与者需先后回答两道选择题,问题A有四个选项,问题B有五个选项,但都只有一个选项是正确的,正确回答问题A可获奖金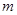 元,正确回答问题B可获奖金
元,正确回答问题B可获奖金 元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
如图1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2。
(1)求证:BC⊥平面A1DC;
(2)若CD=2,求BE与平面A1BC所成角的正弦值。
已知数列 的前
的前 项和为
项和为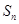 ,
,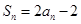 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设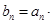 log2an+1 ,求数列
log2an+1 ,求数列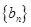 的前
的前 项和
项和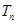 。
。