小白鼠被注射某种药物后,只会表现为以下三种症状中的一种:兴奋、无变化(药物没有发生作用)、迟钝.若出现三种症状的概率依次为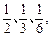 现对三只小白鼠注射
现对三只小白鼠注射 这种药物.
这种药物.
(Ⅰ)求这三只小白鼠表现症状互不相同的概率;
(Ⅱ)用 表示三只小白鼠共表现症状的种数,求
表示三只小白鼠共表现症状的种数,求 的分布列及数学期望
的分布列及数学期望
在 中,
中,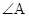 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,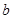 ,
,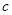 ,若
,若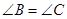 ,且
,且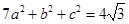 ,求
,求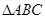 的面积的最大值.
的面积的最大值.
已知数列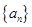 的前
的前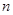 项和
项和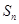 满足
满足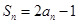 ,等差数列
,等差数列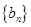 满足
满足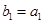 ,
,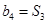 .
.
(1)求数列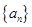 ,
,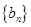 的通项公式;
的通项公式;
(2)设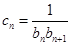 ,求数列
,求数列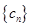 的前
的前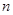 项和
项和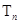 .
.
已知以点C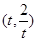 (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(Ⅰ)求证:△AOB的面积为定值;
(Ⅱ)设直线2x+y-4=0与圆C交于点M、N,若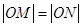 ,求圆C的方程.
,求圆C的方程.
(Ⅲ)在(Ⅱ)的条件下,设P、Q分别是直线l:x+y+2=0和圆C上的动点,求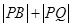 的最小值。
的最小值。
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.
(Ⅰ)若 =
=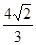 ,求
,求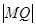 及直线MQ的方程;
及直线MQ的方程;
(Ⅱ)求证:直线AB恒过定点.
三角形ABC的三个顶点A(1,3)B(1,﹣3)C(3,3),求
(Ⅰ)BC边上中线AD所在直线的方程;
(Ⅱ)三角形ABC的外接圆O1的方程;
(Ⅲ)已知圆O2: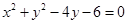 ,求圆心在x-y-4=0,且过圆O1与圆O2交点的圆的方程。
,求圆心在x-y-4=0,且过圆O1与圆O2交点的圆的方程。