在平面直角坐标系xOy中,如图,已知椭圆C: 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
(1)设直线AP、PB的斜率分别为k1,k2,求证:k1·k2为定值;
(2)求线段MN长的最小值;
(3)当点P运动时,以MN为直径的圆是否经过某定点?请证明你的结论.
. 函数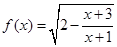 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.
(1)求A;(2)若B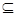 A,求实数
A,求实数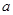 的取值范围。
的取值范围。
已知定义在(-∞,—1)∪(1,+∞)上的奇函数满足:①f(3)=1;②对任意的x>2, 均有f(x)>0,③对任意的x>0,y>0.均有f(x+1)+f(y+1)=f(xy+1)
⑴试求f(2)的值;
⑵证明f(x)在(1,+∞)上单调递增;
⑶是否存在实数a,使得f(cos2θ+asinθ)<3对任意的θ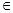 (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ为锐角,且f(θ+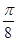 )=
)=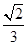 ,求tan2θ的值.
,求tan2θ的值.
已知函数f(x)=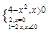
(1)求f(f(-2))的值;
(2)求f(a2+1)(a∈R)的值;
(3)当-4≤x<3时,求函数f(x)的值域.
求函数f(x)="sinx+cosx+sinxcosx." x∈﹝0,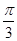 ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.