已知中心在坐标原点,焦点在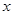 轴上的椭圆过点
轴上的椭圆过点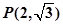 ,且它的离心率
,且它的离心率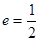 .
.
(Ⅰ)求椭圆的标准方程;
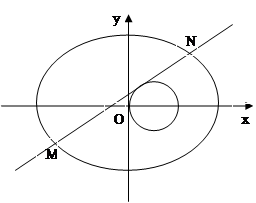
(Ⅱ)与圆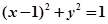 相切的直线
相切的直线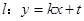 交椭圆于
交椭圆于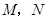 两点,若椭圆上一点
两点,若椭圆上一点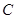 满足
满足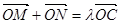 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)若 无极值点,但其导函数
无极值点,但其导函数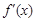 有零点,求
有零点,求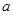 的值;
的值;
(Ⅱ)若 有两个极值点,求
有两个极值点,求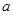 的取值范围,并证明
的取值范围,并证明 的极小值小于
的极小值小于 .
.
已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求a,b满足的关系式;
(2)若 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
(3)证明: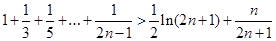 (
(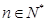 )
)
已知函数
 .
.
(1)讨论函数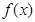 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数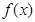 在
在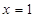 处取得极值,对
处取得极值,对
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)若函数 在区间
在区间 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;
(3)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.

(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.