如图是一个半圆形湖面景点的平面示意图.已知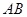 为直径,且
为直径,且 km,
km,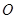 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近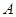 的一点,
的一点,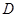 为圆周上靠近
为圆周上靠近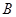 的一点,且
的一点,且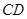 ∥
∥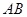 .现在准备从
.现在准备从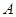 经过
经过 到
到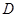 建造一条观光路线,其中
建造一条观光路线,其中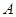 到
到 是圆弧
是圆弧 ,
, 到
到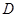 是线段
是线段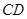 .设
.设 ,观光路线总长为
,观光路线总长为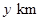 .
.
(1)求 关于
关于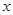 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
如图,在四棱锥 中,底面
中,底面 是菱形,且
是菱形,且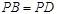 .
.
(1)求证: ;
;
(2)若平面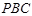 与平面
与平面 的交线为
的交线为 ,求证:
,求证: .
.
已知 的内角
的内角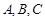 的对边分别为
的对边分别为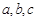 ,
,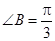 .
.
(1)若 ,
,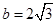 ,求
,求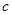 的值;
的值;
(2)若 ,求
,求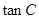 的值.
的值.
已知数列 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有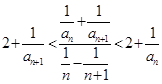 成立,且
成立,且 .
.
(1)求 ,
,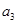 的值;
的值;
(2)猜想数列 的通项公式,并给出证明.
的通项公式,并给出证明.
(本小题满分10分)如图,在直三棱柱 中,已知
中,已知 ,
, ,
, ,点
,点 ,
, 分别在棱
分别在棱 ,
, 上,且
上,且 ,
, ,
, .
. 
(1)当 时,求异面直线
时,求异面直线 与
与 所成角的大小;
所成角的大小;
(2)当直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 时,求
时,求 的值.
的值.