如图，△AGB中，以边AG、AB为边分别作正方形AEFG、正方形ABCD，线段EB和GD相交于点H, tan∠AGB=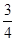
，点G、A、C在同一条直线上.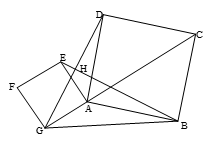
（1）求证：EB⊥GD；
（2）若∠AG=
，求BE的长．
（1）解不等式组：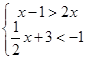
（2）计算：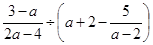
已知抛物线E1：y=x2经过点A（1，m），以原点为顶点的抛物线E2经过点B（2，2），点A、B关于y 轴的对称点分别为点A′，B′．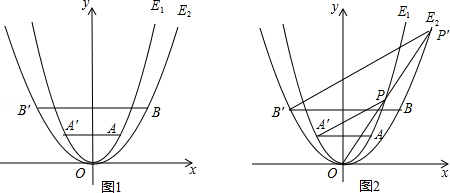
（1）求m的值及抛物线E2所表示的二次函数的表达式；
（2）如图1，在第一象限内，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；
（3）如图2，P为第一象限内的抛物线E1上与点A不重合的一点，连接OP并延长与抛物线E2相交于点P′，求△PAA′与△P′BB′的面积之比．
已知点P是线段AB上与点A不重合的一点，且AP＜PB．AP绕点A逆时针旋转角α（0°＜α≤90°）得到AP1，BP绕点B顺时针也旋转角α得到BP2，连接PP1、PP2．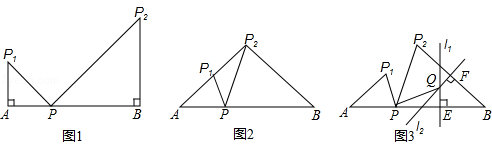
（1）如图1，当α=90°时，求∠P1PP2的度数；
（2）如图2，当点P2在AP1的延长线上时，求证：△P2P1P∽△P2PA；
（3）如图3，过BP的中点E作l1⊥BP，过BP2的中点F作l2⊥BP2，l1与l2交于点Q，连接PQ，求证：P1P⊥PQ．
大学生小刘回乡创办小微企业，初期购得原材料若干吨，每天生产相同件数的某种产品，单件产品所耗费的原材料相同．当生产6天后剩余原材料36吨，当生产10天后剩余原材料30吨．若剩余原材料数量小于或等于3吨，则需补充原材料以保证正常生产．
（1）求初期购得的原材料吨数与每天所耗费的原材料吨数；
（2）若生产16天后，根据市场需求每天产量提高20%，则最多再生产多少天后必须补充原材料？
如图，在▱ABCD中，对角线AC与BD相交于点O，∠CAB=∠ACB，过点B作BE⊥AB交AC于点E．
（1）求证：AC⊥BD；
（2）若AB=14，cos∠CAB=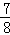
，求线段OE的长．