某公司生产的某种时令商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天）的关系如下表：
| 时间t（天） |
1 |
3 |
6 |
10 |
36 |
… |
| 日销售量m（件） |
94 |
90 |
84 |
76 |
24 |
… |
未来40天内，前20天每天的价格y1（元/件）与时间t（天）的函数关系式为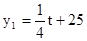
（
且t为整数），后20天每天的价格y2（元/件）与时间t（天）的函数关系式
为
（
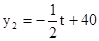且t为整数）. 下面我们就来研究销售这种商品的有关问题：（1）分析上表中的数据，确定一个满足这些数据的m（件）与t（天）之间的关系式；
（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润（a<4）给希望工程. 公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围.
（钦州）某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球（每个气排球的价格都相同，每个篮球的价格都相同）．经洽谈，购买1个气排球和2个篮球共需210元；购买2个气排球和3个篮球共需340元．
（1）每个气排球和每个篮球的价格各是多少元？
（2）该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个，总费用不超过3200元，且购买气排球的个数少于30个，应选择哪种购买方案可使总费用最低？最低费用是多少元？
（来宾）已知购买1个足球和1个篮球共需130元，购买2个足球和1个篮球共需180元．
（1）求每个足球和每个篮球的售价；
（2）如果某校计划购买这两种球共54个，总费用不超过4000元，问最多可买多少个篮球？
（贺州）某商场销售一批同型号的彩电，第一个月售出50台，为了减少库存，第二个月每台降价500元将这批彩电全部售出，已知第一个月的销售额与第二个月的销售额相等，这两个月销售总额超过40万元．
（1）求第一个月每台彩电销售价格；
（2）这批彩电最少有多少台？
（贺州）解分式方程：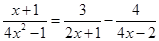
．
（河池）联华商场以150元/台的价格购进某款电风扇若干台，很快售完．商场用相同的货款再次购进这款电风扇，因价格提高30元，进货量减少了10台．
（1）这两次各购进电风扇多少台？
（2）商场以250元/台的售价卖完这两批电风扇，商场获利多少元？