某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s.比赛时.某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.
(1)求空气阻力大小与球速大小的比例系数k;
(2)求在加速跑阶段球拍倾角θ随速度v变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为v0,而球拍的倾角比θ0大了β并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件.
如图,质量为m=5kg的小球穿在斜杆上,斜杆与水平方向的夹角为θ=37°,球恰好能在杆上匀速滑动.若球受到一大小为F=200N的水平推力作用,可使小球沿杆向上加速滑动(g取10m/s2),求:(sin370=0.6 cos370=0.8)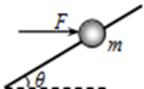
(1)小球与斜杆间的动摩擦因数μ的大小;
(2)小球沿杆向上加速滑动的加速度大小.
经检测某车的刹车性能:以标准速度20m/s在平直公路上行驶时,刹车后做匀减速运动10s停下来。某时刻,某车从静止开始,以减速时一半大小的加速度做匀加速直线运动,达到20m/s速度时立即刹车直至停下。求该车从静止开始加速,最后又停下的整个过程中:
(1)该车运动的总时间。
(2)该车前行的总位移。
(10分)如图所示,小车在水平路面上加速向右运动,用一条水平绳和一条斜绳(斜绳与竖直方向的夹角θ=30°)把一个质量为m的小球系于车内.不计绳的质量,求下列两种情况下,两绳对小球的拉力大小: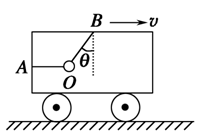
(1)小车以加速度a1=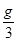 运动;
运动;
(2)小车以加速度a2=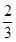 g运动.
g运动.
如图所示,质量M=8 kg的小车放在光滑水平面上,在小车左端加一水平推力F=8 N。当小车向右运动的速度达到3 m/s时,在小车右端轻轻地放一个大小不计、质量m=2 kg的小物块。小物块与小车间的动摩擦因数μ=0.2,小车足够长。g取10 m/s2,则: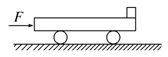
(1)放上小物块后,小物块及小车的加速度各为多大;
(2)经多长时间两者达到相同的速度;
如图所示,质量m=0.5kg的物体放在水平面上,在F=3.0N的水平恒定拉力作用下由静止开始运动,物体发生位移x=4.0m时撤去力F,物体在水平面上继续滑动一段距离后停止运动。已知物体与水平面间的动摩擦因数μ=0.4, g=10m/s2。求: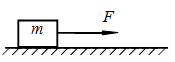
(1)物体在力F作用过程中加速度的大小;
(2)撤去力F的瞬间,物体速度的大小;
(3)撤去力F后物体继续滑动的时间。