如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成直二面角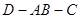 ,如图二,在二面角
,如图二,在二面角 中.
中.
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(1)该考生得40分的概率;
(2)该考生得多少分的可能性最大?
(3)该考生所得分数的数学期望.
已知:函数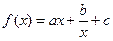 (
(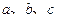 是常数)是奇函数,且满足
是常数)是奇函数,且满足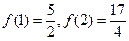 ,
,
(Ⅰ)求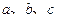 的值;
的值;
(Ⅱ)试判断函数 在区间
在区间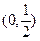 上的单调性并说明理由;
上的单调性并说明理由;
(Ⅲ)试求函数 在区间
在区间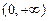 上的最小值.
上的最小值.
已知数列{an}、{bn}满足:a1=1,a2=a(a为实数),且 ,其中n=1,2,3,…
,其中n=1,2,3,…
(Ⅰ)求证:“若数列{an}是等比数列,则数列{bn}也是等比数列”是真命题;
(Ⅱ)写出(Ⅰ)中命题的逆命题;判断它是真命题还是假命题,并说明理由.
设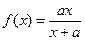
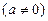 ,令
,令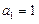 ,
,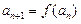 ,又
,又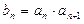 ,
,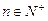 .
.
(Ⅰ)判断数列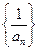 是等差数列还是等比数列并证明;
是等差数列还是等比数列并证明;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)求数列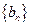 的前
的前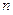 项和.
项和.
已知在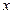 轴上有一点列:
轴上有一点列: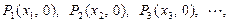
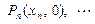 ,点
,点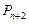 分有向线段
分有向线段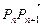 所成的比为
所成的比为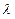 ,其中
,其中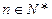 ,
,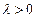 为
为
常数,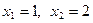 .
.
(1)设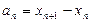 ,求数列
,求数列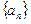 的通项公式;
的通项公式;
(2)设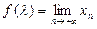 ,当
,当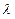 变化时,求
变化时,求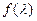 的取值范围.
的取值范围.