如图,在平面直角坐标系中,点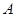 是反比例函数
是反比例函数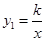
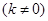 图象上一点,
图象上一点,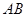 ⊥
⊥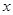 轴于
轴于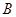 点,一次函数
点,一次函数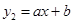
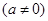 的图象交
的图象交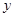 轴于
轴于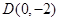 ,交
,交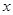 轴于
轴于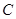 点,并与反比例函数的图象交于
点,并与反比例函数的图象交于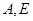 两点,连接
两点,连接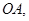 若△
若△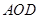 的面积为4,且
的面积为4,且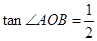 .
.
(1) 分别求出该反比例函数和一次函数的解析式;
(2) 求△ 的面积.
的面积.
(本题4分)下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京的时间早的时数)。现在的北京时间是上午9∶00
| 城市 |
时差/ 时 |
| 纽约 |
-13 |
| 巴黎 |
-7 |
| 东京 |
+1 |
| 芝 加 哥 |
-14 |
(1)求现在纽约时间是多少?
(2)斌斌现在想给远在巴黎的姑妈打电话,你认为合适吗?
(本题6分)把下列4数在数轴上表示出来,并按从小到大的顺序用“<”连接起来。
3.5,-0.75,-2 ,
, 
(第一题6分第二题7分)
(1)有理数a,b,c在数轴上的位置如图所示,且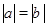 ,化简
,化简 .
.
(2) 与
与 是同类项,求代数式:3x2-6y2+3(xy-3y2)-(3x2+3xy+7y2)的值.
是同类项,求代数式:3x2-6y2+3(xy-3y2)-(3x2+3xy+7y2)的值.
为了有效控制酒后驾车,吉安市城管的汽车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:(单位:千米)
+2,-3,+2,+1,-2,-1,-2.
(1)此时,这辆城管的汽车司机如何向队长描述他的位置?
(2)如果队长命令他马上返回出发点,这次巡逻(含返回)共耗油多少升(已知每千米耗油0.2升)?
a,b互为相反数,c、d互为倒数,m的绝对值是1,则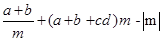 的值?
的值?