在Rt△ABC中,∠C=90°,∠A=30°,BC=2.若将此直角三角形的一条直角边BC或AC与x轴重合,使点A或点B刚好在反比例函数  (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.将线段AB绕点B顺时针旋转90°,得线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.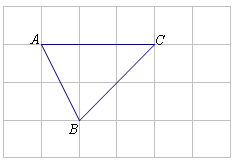
(Ⅰ)作出旋转后的图形;
(Ⅱ)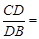 ________.
________.
如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D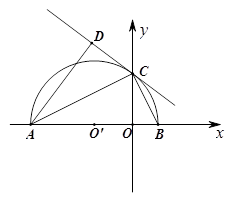
(1)求证:∠CAD =∠CAB
(2)已知抛物线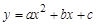 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=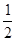 .
.
① 求抛物线的解析式
② 判断抛物线的顶点E是否在直线CD上,并说明理由;
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
(1)求一张画板的出售价与边长之间满足的函数关系式
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式。
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
如图,AB是⊙O的直径,C、D在⊙O上,连结BC,过D作PF∥AC交AB于E,交⊙O于F,交BC于点G,交过B点的直线于点P,且∠BPF=∠ADC.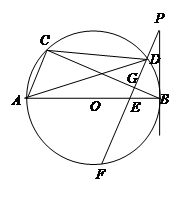
(1)判断直线BP与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为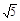 ,AC=2,BE=1,求BP的长.
,AC=2,BE=1,求BP的长.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B。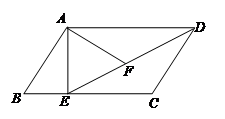
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6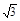 ,AF=4
,AF=4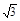 ,求AE的长。
,求AE的长。