(1)﹣8a2b+2a3+8ab2; (2)(x+y)2+2(x+y)+1;
(3)x2(x﹣y)+(y﹣x); (4)x2﹣2xy+y2﹣9.
我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
(2)如图, 中, ,点 在 上,且 ,求证: 是 的“内似线”;
(3)在 中, , , , 、 分别在边 、 上,且 是 的“内似线”,求 的长.
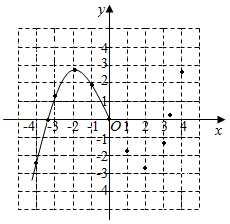
某学习小组在研究函数 的图象与性质时,已列表、描点并画出了图象的一部分.
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
3.5 |
4 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
(1)请补全函数图象;
(2)方程 实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.
不透明袋子中装有2个红球,1个白球和1个黑球,这些球除颜色外无其他差别,随机摸出1个球不放回,再随机摸出1个球,求两次均摸到红球的概率.
张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择.如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买 个甲种文具时,需购买 个乙种文具.
(1)①当减少购买1个甲种文具时, , ;
②求 与 之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元.甲、乙两种文具各购买了多少个?
全面两孩政策实施后,甲、乙两个家庭有了各自的规划,假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.