如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB.类似地,在AB上折出点B″使AB″=AB′.这时B″就是AB的黄金分割点.请你证明这个结论.
在直角坐标系中,标出下列各点的位置,并写出各点的坐标.
(1)点A在x轴上,位于原点的左侧,距离坐标原点4个单位长度;
(2)点B在y轴上,位于原点的上侧,距离坐标原点4个单位长度;
(3)点C在y轴的左侧,在x轴的上侧,距离每个坐标轴都是4个单位长度.
请大家在坐标纸上建立直角坐标系,并进行描点.
图是动物园的平面示意图,O、A、B、C、D、E分别表示大门、熊猫馆、水族馆、鸟类馆、猴山和河马馆.其中用(0,0)表示点O,用(2,4)表示点A.请借助刻度尺、量角器解决如下问题: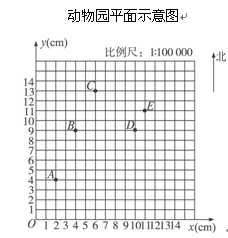
(1)量出A、B、C、D的图上坐标.
(2)位于原点东偏北45°的是哪个馆,它到原点(大门)的实际距离是多少?
在直角坐标系中描出下列各点,并将各组内的点用线段顺次连结起来.
(1)(-9,7),(-6,7);
(2)(-9,4),(-6,4);
(3)(-6,1),(-6,11);
(4)(-4,11),(-4,1),(-1,1),(-1,2);
(5)(-4,4),(-2,7);
(6)(3,11),(4,10);
(7)(1,10),(7,10);
(8)(2,8),(6,8),(6,6),(2,6),(2,8);
(9)(4,6),(4,1),(3,2);
(10)(1, 2),(3,4);
(11)(5,4),(7,2).
观察所得的图形,你觉得它像什么?
如图所示的是一长方形纸板,请你把它裁成两块,然后拼成一个正方形,你能做到吗?请画图说明.
在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
(1)分别求出线段AB中点,线段AC中点及线段CD中点的坐标,则线段AB 中点的坐标与点A,B的坐标之间有什么关系?对线段AC中点和点A,C及线段CD中点和点C,D成立吗?
(2)已知点M(a,0),N(b,0),请写出线段MN的中点P的坐标.