已知数列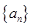 的相邻两项
的相邻两项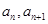 是关于
是关于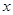 的方程
的方程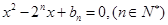 的两根,且
的两根,且 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列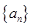 的前
的前 项和
项和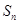 ;
;
(Ⅲ)设函数 若
若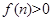 对任意的
对任意的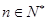 都成立,求
都成立,求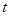 的取值范围。
的取值范围。
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500))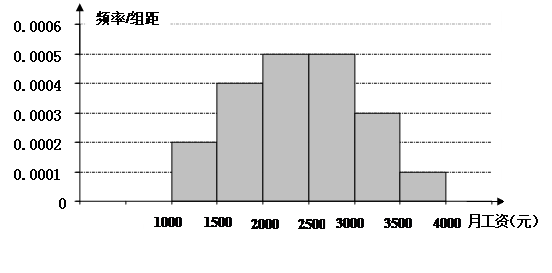
(I)求居民收入在[3000,3500)的频率
(II)根据频率分布直方图算出样本数据的中位数;
(III)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在[2500,3000)的这段应抽取多少人?
已知 ,求证:
,求证: 。
。
已知关于 的不等式
的不等式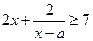 在
在 上恒成立,求实数
上恒成立,求实数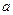 的最小值;
的最小值;
已知函数 .
.
(1)求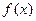 的导数
的导数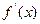 ;
;
(2)求证:不等式 上恒成立;
上恒成立;
(3)求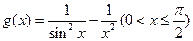 的最大值。
的最大值。
在一次食品卫生大检查中,执法人员从抽样中得知,目前投放我市的甲、乙两种食品的合格率分别为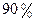 和
和 。
。
(1)今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
(2)若某消费者从两种食品中任意各购一件,设 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出 的分布列,并求其数学期望.
的分布列,并求其数学期望.