某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，（每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500））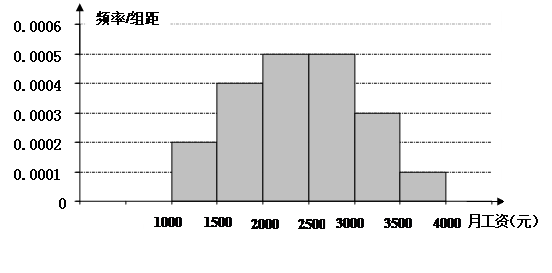
（I）求居民收入在[3000，3500）的频率
（II）根据频率分布直方图算出样本数据的中位数；
（III）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析，则月收入在[2500，3000）的这段应抽取多少人？
过点Q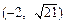 
作圆C：x2＋y2＝r2(
)的切线，切点为D，且QD＝4．
(1)求r的值；
(2)设P是圆C上位于第一象限内的任意一点，过点P作圆C的切线l，且l交x轴于点A，交y 轴于点B，设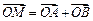
，求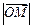
的最小值(O为坐标原点).
如图，已知三棱柱ABC－A1B1C1中，侧棱A A1⊥底面ABC
AB⊥BC；
（Ⅰ）求证：平面A1BC⊥侧面A1ABB1.
（Ⅱ）若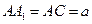
,直线AC与平面A1BC所成的角为
，
求AB的长。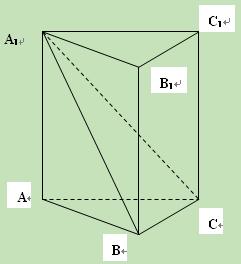
已知数列
的首项为
=3，通项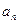
与前n项和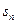
之间满足2=·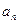
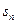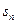
（n≥2）。
(1)求证：
是等差数列，并求公差；
(2)求数列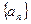的通项公式。
设△ABC的内角A，B，C的对边分别为a,b,c.已知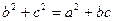
，求：
（Ⅰ）A的大小;
（Ⅱ）若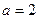
，求
面积的最大值.
如图，在长为52宽为42的大矩形内有一个边长为18的小正方形，现向大矩形内
随机投掷一枚半径为1的圆片，求：
（Ⅰ）圆片落在大矩形内部时，其圆心形成的图形面积；
（Ⅱ）圆片与小正方形及内部有公共点的概率．