(本小题满分10分)选修4-1:几何证明选讲
如图,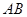 是圆
是圆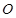 的直径,
的直径,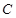 是半径
是半径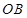 的中点,
的中点,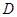 是
是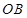 延长线上一点,且
延长线上一点,且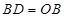 ,直线
,直线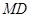 与圆
与圆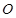 相交于点
相交于点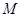 、
、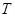 (不与
(不与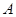 、
、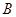 重合),
重合),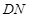 与圆
与圆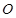 相切于点
相切于点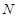 ,连结
,连结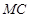 ,
,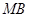 ,
,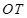 .
.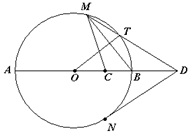
(Ⅰ)求证: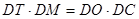 ;
;
(Ⅱ)若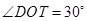 ,求
,求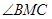 .
.
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为
各人是否需使用设备相互独立.
(1)求同一工作日至少3人需使用设备的概率;
(2)
表示同一工作日需使用设备的人数,求
的数学期望.
如图,三棱柱
中,点
在平面
内的射影
在
上,
,
.
(1)证明:
;
(2)设直线
与平面
的距离为
,求二面角
的大小.
等差数列
的前
项和为
,已知
为整数,且
.
(1)求
的通项公式;
(2)设
,求数列
的前
项和
.
的内角 的对边分别为 ,已知 , ,求 .
对于数对序列
,记
,
,其中
表示
和
两个数中最大的数.
(1)对于数对序列
,求
的值;
(2)记 为 四个数中最小的数,对于由两个数对 组成的数对序列 和 ,试分别对 和 两种情况比较 和 的大小;(3)在由五个数对 组成的所有数对序列中,写出一个数对序列 使 最小,并写出 的值.(只需写出结论).