某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| |
甲班 (A方式) |
乙班 (B方式) |
总计 |
| 成绩优秀 |
|
|
|
| 成绩不优秀 |
|
|
|
| 总计 |
|
|
|
附: 
 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k |
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |
(本小题共12分)已知数列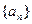 的前n项和
的前n项和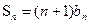 ,其中
,其中 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,
(1)求数列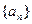 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列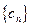 的前n项和
的前n项和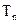
(本小题共12分)直四棱柱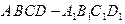 中,底面是边长为
中,底面是边长为 的正方形,侧棱长为4。
的正方形,侧棱长为4。
(1)求证:平面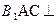 平面
平面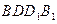 ;
;
(2)求点 到平面
到平面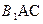 的距离d;
的距离d;
(3)求三棱锥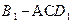 的体积V。
的体积V。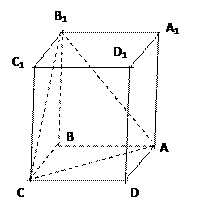
(本小题共12分)如图,在四棱锥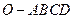 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
, 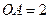 ,
,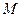 为
为 的中点,
的中点, 为
为 的中点,求异面直线OC与MN所成角的余弦值。
的中点,求异面直线OC与MN所成角的余弦值。
已知数列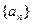 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,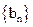 是首项为1,公比为3的等比数列,
是首项为1,公比为3的等比数列,
(1)求数列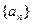 、
、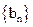 的通项公式 ;(2)求数列
的通项公式 ;(2)求数列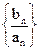 的前n项和
的前n项和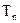 。
。
如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2, G是PB的中点。
①证明:PD// 面AGC;
②求AG和平面PBD所成的角的正切值。
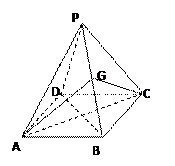 |