如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2, G是PB的中点。
①证明:PD// 面AGC;
②求AG和平面PBD所成的角的正切值。
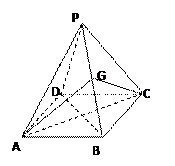 |
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.9,则P(0<ξ<2)=( )
| A.0.2 | B.0.3 | C.0.4 | D.0.6 |
已知函数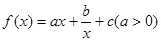 的图象在点
的图象在点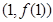 处的切线方程为
处的切线方程为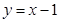 .[来
.[来
(1)用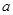 表示出
表示出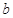 ,
,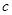 ;
;
(2)证明:当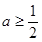 时,
时,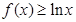 在
在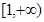 上恒成立;
上恒成立;
(3)证明: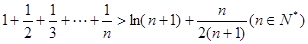 .
.
设F1,F2分别是椭圆C: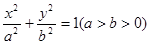 的左、右焦点.
的左、右焦点.
(1)设点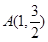 是椭圆C上的点,且F1(﹣1,0),F2(1,0),试写出椭圆C的方程;
是椭圆C上的点,且F1(﹣1,0),F2(1,0),试写出椭圆C的方程;
(2)设K是(1)中所得椭圆上的动点,求线段 的中点B的轨迹方程;
的中点B的轨迹方程;
(3)设点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M、N两点,若直线PM,PN的斜率都存在,并记为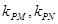 ,试探究
,试探究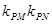 的值是否与点P及直线L有关,并证明你的结论.
的值是否与点P及直线L有关,并证明你的结论.
在数列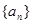 ,
,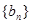 中,
中,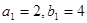 且
且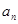 ,
,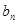 ,
, 成等差数列,
成等差数列,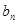 ,
, ,
,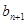 成等比数列(
成等比数列(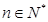 ).
).
(1)求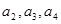 及
及 ;
;
(2)猜想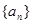 ,
,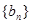 的通项公式,并证明你的结论.
的通项公式,并证明你的结论.
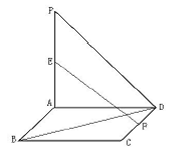
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求EF和平面ABCD所成的角α的正切;
(Ⅲ)求异面直线EF与BD所成的角β的余弦.