已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.9,则P(0<ξ<2)=( )
| A.0.2 | B.0.3 | C.0.4 | D.0.6 |
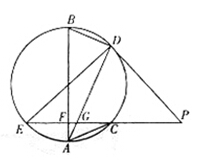
如图,
交圆于
、
两点,
切圆于
为
上一点且
,连接
并延长交圆于点
,作弦
垂直
,垂足为
.
(1)求证:
为圆的直径;
(2)若
,求证:
.
已知函数 , .证明:
(1)存在唯一
,使
;
(2)存在唯一
,使
,且对(1)中的
.
圆
的切线与
轴正半轴,
轴正半轴围成一个三角形,当该三角形面积最小时,切点为
(如图),双曲线
过点
且离心率为
.
(1)求
的方程;
(2)椭圆
过点P且与
有相同的焦点,直线
过
的右焦点且与
交于
两点,若以线段
为直径的圆心过点
,求
的方程.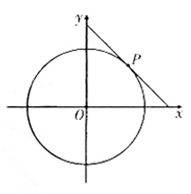
如图,
和
所在平面互相垂直,且
,
,
分别为
的中点.
(1)求证:
;
(2)求二面角
的正弦值.
一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示: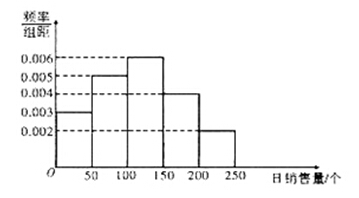
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率;
(2)用
表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望
及方差
.