已知函数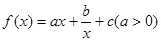 的图象在点
的图象在点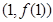 处的切线方程为
处的切线方程为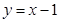 .[来
.[来
(1)用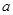 表示出
表示出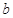 ,
,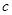 ;
;
(2)证明:当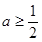 时,
时,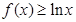 在
在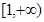 上恒成立;
上恒成立;
(3)证明: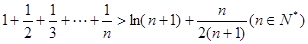 .
.
(本小题满分8分)已知数列 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列 的前
的前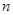 项和
项和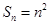 .
.
(1)求数列 与
与 的通项公式;(2)求数列
的通项公式;(2)求数列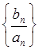 的前
的前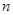 项和.
项和.
(本小题满分8分)如图5,在四棱锥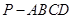 中,底面
中,底面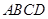 为正方形,
为正方形, 平面
平面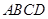 ,
, ,点
,点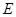 是
是 的中点.(1)求证:
的中点.(1)求证: 平面
平面 ;
;
(2)若四面体 的体积为
的体积为 ,求
,求 的长.
的长.
(本小题满分8分) 某校在高二年级开设了 ,
, ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从 ,
, ,
, 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 |
小组人数 |
抽取人数 |
 |
24 |
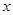 |
 |
36 |
3 |
 |
48 |
 |
(1)求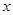 ,
, 的值;
的值;
(2)若从 ,
, 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组 的概率.
的概率.
(本小题满分6分)在△ 中,角
中,角 ,
, ,
, 成等差数列.
成等差数列.
(1)求角 的大小;(2)若
的大小;(2)若 ,求
,求 的值.
的值.
已知数列{an},a1=2a+1(a≠-1的常数),an=2an-1+n2-4n+2(n≥2,n∈N∗),数列{bn}的首项, b1=a,bn=an+n2(n≥2,n∈N∗).
(1)证明:{bn}从第2项起是以2为公比的等比数列并求{bn}通项公式;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;(3)当a>0时,求数列{an}的最小项.