(本小题满分12分)
某矩形花园 ,
,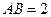 ,
,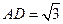 ,
, 是
是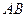 的中点,在该花园中有一花圃其形状是以
的中点,在该花园中有一花圃其形状是以 为直角顶点的内接Rt△
为直角顶点的内接Rt△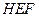 ,其中E、F分别落在线段
,其中E、F分别落在线段 和线段
和线段 上如图.分别记
上如图.分别记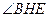 为
为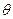 (
( ),
),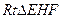 的周长为
的周长为 ,
,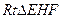 的面积为
的面积为
(1)试求 的取值范围;
的取值范围;
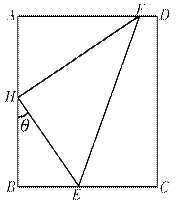
(2)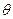 为何值时
为何值时 的值为最小;并求
的值为最小;并求 的最小值.
的最小值.
已知抛物线C:y2=2px(p>0)的焦点F和椭圆 的右焦点重合,直线
的右焦点重合,直线 过点F交抛物线于A、B两点.
过点F交抛物线于A、B两点.
(1)求抛物线C的方程;
(2)若直线 交y轴于点M,且
交y轴于点M,且 ,m、n是实数,对于直线
,m、n是实数,对于直线 ,m+n是否为定值?
,m+n是否为定值?
若是,求出m+n的值;否则,说明理由.
在四棱锥P-ABCD中,侧面PCD 底面ABCD,PD
底面ABCD,PD CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC, ,
, ,
, .
.
(1)求证:BC 平面PBD:
平面PBD:
(2)求直线AP与平面PDB所成角的正弦值;
(3)设E为侧棱PC上异于端点的一点, ,试确定
,试确定 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为 .
.
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
已知向量 ,函数
,函数 .
.
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)已知 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
,
求 的面积.
的面积.
已知 是公差不等于0的等差数列,
是公差不等于0的等差数列, 是等比数列
是等比数列 ,且
,且 .
.
(1)若 ,比较
,比较 与
与 的大小关系;
的大小关系;
(2)若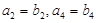 .(ⅰ)判断
.(ⅰ)判断 是否为数列
是否为数列 中的某一项,并请说明理由;
中的某一项,并请说明理由;
(ⅱ)若 是数列
是数列 中的某一项,写出正整数
中的某一项,写出正整数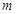 的集合(不必说明理由).
的集合(不必说明理由).