如图,已知直线 与双曲线
与双曲线 交于A(
交于A( ),B(
),B( )两点(A与B不重合),直线AB与
)两点(A与B不重合),直线AB与 轴交于P(
轴交于P( ),与
),与 轴交于点C.
轴交于点C.
(1)若A,B两点的坐标分别为(1,3),(3,y2).求点P的坐标;
(2)若 ,点
,点 的坐标为(6,0),且
的坐标为(6,0),且 .求
.求 两点的坐标;
两点的坐标;
(3)结合(1),(2)中的结果,猜想并用等式表示 之间的关系(不要求证明).
之间的关系(不要求证明).
(本小题满分12分)
如图,在边长为a的正方体 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、 、
、 的中点.
的中点.
(1)求点P到平面MNQ的距离;
(2)求直线PN与平面MPQ所成角的正弦值.
(本小题满分13分)
如图PA⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB,PD的中点.
(1)求证:AF//平面PCE;
(2)若PA=AD且AD=2,CD=3,求P—CE—A的正切值.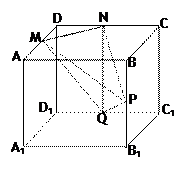
(本小题满分13分)
某军事院校招生要经过考试和体检两个过程,在考试通过后才有体检的机会,两项都合格则被录取.若甲、乙、丙三名考生能通过考试的概率分别为0.4,0.5,0.8,体检合格的概率分别为0.5,0.4,0.25,每名考生是否被录取相互之间没有影响.
(1)求恰有一人通过考试的概率;
(2)设被录取的人数为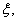 求
求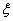 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)
已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)设 ,求
,求 的值域和单调递增区间.
的值域和单调递增区间.
本小题满分12分)
如图点 为双曲线
为双曲线 的左焦点,左准线
的左焦点,左准线 交
交 轴于点
轴于点 ,点P是
,点P是 上的一点
上的一点 ,且线段PF的中点
,且线段PF的中点 在双曲线
在双曲线 的左支上.
的左支上.
(1)求双曲线 的标准方程;
的标准方程;
(2)若过点 的直线
的直线 与双曲线
与双曲线 的左右两支分别交于
的左右两支分别交于 、
、 两点,设
两点,设 ,当
,当 时,求直线
时,求直线 的斜率
的斜率 的取值范围.
的取值范围. 