(本小题满分10分)选修4-5:不等式选讲
设不等式 的解集为A,且
的解集为A,且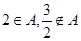
(Ⅰ)求a的值;
(Ⅱ)求函数 的最小值。
的最小值。
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是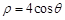 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: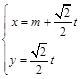 (
( 是参数).
是参数).
(Ⅰ)若直线l与曲线C相交于A、B两点,且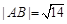 ,试求实数m值.
,试求实数m值.
(Ⅱ)设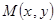 为曲线
为曲线 上任意一点,求
上任意一点,求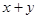 的取值范围.
的取值范围.
(本小题满分12分)椭圆C: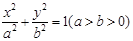 的长轴是短轴的两倍,点
的长轴是短轴的两倍,点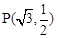 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为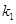 、
、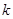 、
、 ,且
,且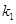 、
、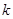 、
、 恰好构成等比数列,记△
恰好构成等比数列,记△ 的面积为S.
的面积为S.
(Ⅰ)求椭圆C的方程.
(Ⅱ)试判断 是否为定值?若是,求出这个值;若不是,请说明理由?
是否为定值?若是,求出这个值;若不是,请说明理由?
(Ⅲ)求S的范围.
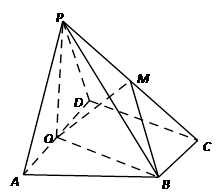
(本小题满分12分)如图,在四棱锥 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,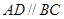 ,
, ,平面
,平面 ⊥底面
⊥底面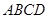 ,
, 为
为 的中点,
的中点,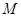 是棱
是棱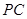 上的点,
上的点, ,
,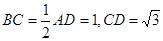 ,
,
(Ⅰ)若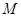 是棱
是棱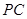 的中点,求证:
的中点,求证: ;
;
(Ⅱ)求证:若二面角M-BQ-C为30°,试求 的值。
的值。
(本小题满分12分)设双曲线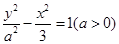 的两个焦点分别为
的两个焦点分别为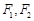 ,离心率为2.
,离心率为2.
(Ⅰ)求此双曲线的渐近线 的方程;
的方程;
(Ⅱ)若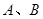 分别为
分别为 上的点,且2|AB|=5|F1F2|,求线段
上的点,且2|AB|=5|F1F2|,求线段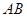 的中点M的轨迹方程,并说明轨迹是什么曲线。
的中点M的轨迹方程,并说明轨迹是什么曲线。