为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为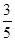 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式:
参考数据:
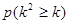 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
在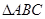 中,角
中,角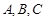 所对的边分别为
所对的边分别为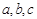 ,若
,若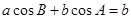 。
。
(1)求证 ;
;
(2)若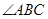 的平分线交
的平分线交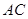 于
于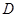 ,且
,且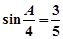 ,求
,求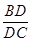 的值。
的值。
已知函数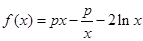 .
.
(1)若p=2,求曲线 处的切线方程;
处的切线方程;
(2)若函数在其定义域内是增函数,求正实数p的取值范围;
(3)设函数 ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点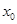 ,使得
,使得 成立,求实
成立,求实
数p的取值范围.
已知函数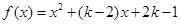 .
.
(1)若 ,函数
,函数 是R上的奇函数,当
是R上的奇函数,当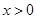 时
时 ,
,
(i)求实数 与
与 的值;
的值;
(ii)当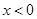 时,求
时,求 的解析式;
的解析式;
(2)若方程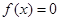 的两根中,一根属于区间
的两根中,一根属于区间 ,另一根属于区间
,另一根属于区间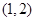 ,求实数
,求实数 的
的
取值范围.
已知函数 在
在 与
与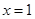 时都取得极值.
时都取得极值.
(1)求 的值与函数
的值与函数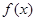 的单调区间;
的单调区间;
(2)若对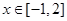 ,不等式
,不等式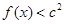 恒成立,求
恒成立,求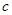 的取值范围.
的取值范围.
函数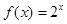 和
和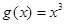 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
(1)请指出示意图中曲线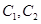 分别对应哪一个函数?
分别对应哪一个函数?
(2) ,且
,且 ,指出
,指出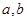 的值,并说明理由;
的值,并说明理由;
(3)结合函数图像示意图,请把
四个数按从小到大的顺序排列.