已知函数 在
在 与
与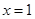 时都取得极值.
时都取得极值.
(1)求 的值与函数
的值与函数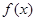 的单调区间;
的单调区间;
(2)若对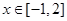 ,不等式
,不等式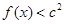 恒成立,求
恒成立,求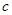 的取值范围.
的取值范围.
已知直线C1: (t为参数),C2:
(t为参数),C2: (θ为参数).
(θ为参数).
(1)当α= 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(2)过坐标原点O作C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
已知曲线C的极坐标方程为ρ=6sinθ,以极点为原点、极轴为x轴非负半轴建立平面直角坐标系,直线l的参数方程为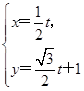 (t为参数),求直线l被曲线C截得的线段的长度.
(t为参数),求直线l被曲线C截得的线段的长度.
已知极坐标方程为ρcosθ+ρsinθ-1=0的直线与x轴的交点为P,与椭圆 (θ为参数)交于点A、B,求PA·PB的值.
(θ为参数)交于点A、B,求PA·PB的值.
在极坐标系中,圆C的方程为ρ=2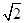 sin
sin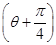 ,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为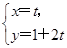 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
在平面直角坐标系xOy中,直线l的参数方程为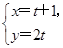 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为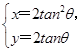 (θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.