抛物线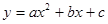 的图像于x轴交于点M
的图像于x轴交于点M ,N
,N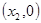 ,且经过点A(0,1),其中
,且经过点A(0,1),其中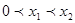 ,过点A的直线
,过点A的直线 交x轴于C点,与抛物线交于点B(异于A点),满足△CAN是等腰直角三角形,且
交x轴于C点,与抛物线交于点B(异于A点),满足△CAN是等腰直角三角形,且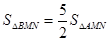 ,求解析式.
,求解析式.
如图1,已知Rt△ABC中,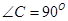 ,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题: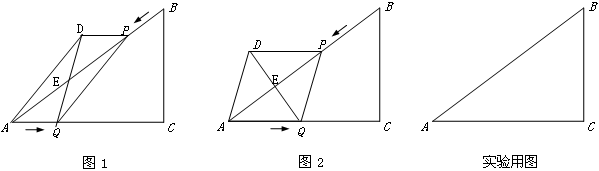
(1)用含有t的代数式表示AE=_____________;
(2)当t为何值时,DQ=AP;
(3)如图2,当t为何值时,平行四边形AQPD为菱形;
(4)直接写出:当DQ的长最小时,t的值.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC交AC的延长线于点E,OE交AD于点F。
(1)求证:DE是⊙O的切线;
(2)若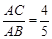 ,求
,求 的值;
的值;
(3)在(2)的条件下,若⊙O直径为10,求△EFD的面积.
某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
关于x的方程kx2+(k+2)x+ =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)当k=4时方程的两根分别为x1 、x2,直接写出x1 +x2 ,x1 x2的值;
(3)是否存在实数k使方程的两个实数根的倒数和等于0?若存在,求出k的值,若不存在,说明理由。
某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC =10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
(1)求∠ADB的度数:
(2)过D点作AB的垂线,垂足为G,求DG的长及索道AB的长.(结果保留根号)