一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个。例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个。
(1)根据题意,完成下表:
| 车站序号 |
在第x车站启程时邮政车厢邮包总数 |
| 1 |
n-1 |
| 2 |
(n-1)-1+(n-2)=2(n-2) |
| 3 |
2(n-2)-2+(n-3)=3(n-3) |
| 4 |
|
| 5 |
|
| … |
…… |
| n |
|
(2)根据上表,写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、
n表示)。
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
已知抛物线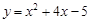 .
.(1)直接写出它与x轴、y轴的交点的坐标;
(2)用配方法将
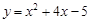 化成
化成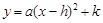 的形式.
的形式.
已知关于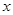 的方程
的方程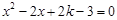 有两个不相等的实数根.
有两个不相等的实数根.(1)求
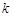 的取值范围;
的取值范围;(2)若
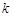 为符合条件的最大整数,求此时方程的根.
为符合条件的最大整数,求此时方程的根.
阅读下列解题过程: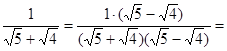
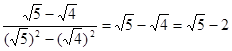
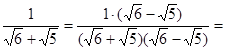
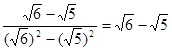
请回答下列问题:(1)观察上面的解题过程,请直接写出
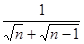 的结果为___________________.
的结果为___________________.(2)利用上面所提供的解法,请化简:
 ……
……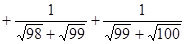
2008年5月l2号,四川省汶川等地发生强烈地震。在抗震救灾中,甲、乙两重灾区急需一批大型挖掘机,甲地需25台,乙地需23台;A、B两省获知情况后慷慨相助,分别捐赠挖掘机26台和22台并将其全部调往灾区。若从A省调运一台挖掘机到甲地要耗资0.4万元,到乙地要耗资0.3万元;从B省调运一台挖掘机到甲地要耗资0.5万元,到乙地要耗资0.2万元。设从A省调往甲地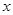 台,A、B两省将捐赠的挖掘机全部调往灾区共耗资
台,A、B两省将捐赠的挖掘机全部调往灾区共耗资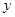 万元。
万元。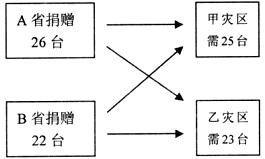
(1)求出
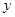 与
与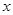 之间的函数关系式及自变量
之间的函数关系式及自变量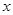 的取值范围;
的取值范围;(2)若要使总耗资不超过15万元,有哪几种调运方案?
(3)怎样设计调运方案使总耗资最少?最少耗资是多少万元?
如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,BC=AD,请说明:OA=OC的道理,小明动手测量了一下,发现OA确实与OC相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看。