(本小题10分)已知抛物线 .
.
(1)求它的对称轴与 轴交点
轴交点 的坐标;
的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与 轴的交点为
轴的交点为 ,
, ,与
,与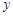 轴的交点为
轴的交点为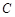 ,若
,若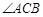 =90°,求此时抛物线的解析式;
=90°,求此时抛物线的解析式;
(3)若点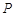 (
(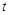 ,
,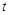 )在抛物线上,则称点
)在抛物线上,则称点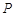 为抛物线的不动点.将抛物线
为抛物线的不动点.将抛物线 进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线 上,请说明理由.
上,请说明理由.
已知反比例函数 的图象与一次函数
的图象与一次函数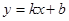 的图象交于点
的图象交于点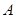 (
(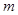 ,2),点
,2),点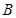 (-2,
(-2, 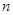 ),一次函数图象与
),一次函数图象与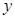 轴的交点为
轴的交点为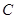 .
.求一次函数解析式;
求
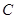 点的坐标;
点的坐标;求△
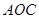 的面积.
的面积.
如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.(1)当AD=3时,求DE的长;
(2)当点
 E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设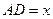 ,
, ,
,
求 关于
关于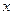 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;(3)在点E、F移动过
 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.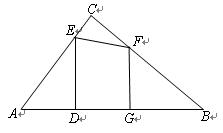
一元二次方程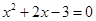 的二根
的二根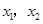 (
(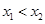 )
)
是抛物线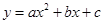 与
与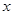 轴的两个交点
轴的两个交点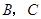 的横坐标,
的横坐标,
且此抛物线过点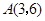 .
.(1)求此二次函数的解析式.
(2)用配方法求此抛物线的顶点为
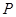 .对称轴
.对称轴(3)当x取什么值时, y随x增大而减小?
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.(1)求平均每天销售量
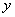 (箱)与销售价
(箱)与销售价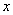 (元
(元 /箱)之间的函数关系式.
/箱)之间的函数关系式.(2)求该批发商平均每天的销售利润
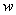 (元)与销售价
(元)与销售价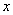 (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
如图,一次函数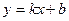 的图象与反比例函数
的图象与反比例函数 图象交于A(-2,1)、B(1,n)两点。
图象交于A(-2,1)、B(1,n)两点。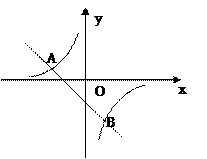
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。