(本小题10分)
如图①,将两个完全相同的三角形纸片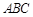 和
和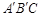 重合放置,其中
重合放置,其中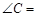 90°,
90°,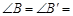 30°,
30°, .
.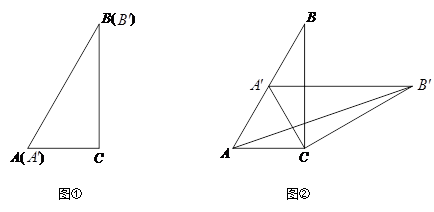
(1)操作发现
如图②,固定△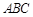 ,将△
,将△ 绕点
绕点 旋转,当点
旋转,当点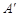 恰好落在
恰好落在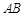 边上时,m]
边上时,m]
①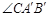 = °,旋转角α= °(0<α<90),线段
= °,旋转角α= °(0<α<90),线段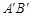 与
与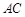 的位置关系是 ;
的位置关系是 ;
②设△ 的面积为
的面积为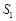 ,△
,△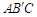 的面积为
的面积为 ,则
,则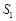 与
与 的数量关系是 ;
的数量关系是 ;
(2)猜想论证
当△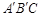 绕点
绕点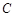 旋转到图③所示的位置时,小明猜想(Ⅰ)中
旋转到图③所示的位置时,小明猜想(Ⅰ)中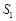 与
与 的数量关系仍然成立,并尝试分别作出了△
的数量关系仍然成立,并尝试分别作出了△ 和△
和△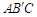 中
中 ,
, 边上的高
边上的高 ,
, ,请你证明小明的猜想;
,请你证明小明的猜想;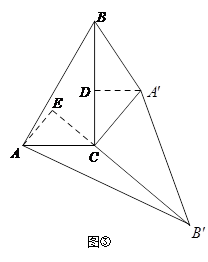
(3)拓展探究
如图④,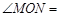 60°,
60°,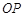 平分
平分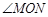 ,
,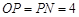 ,
, ∥
∥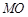 交
交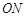 于点
于点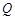 .若在射线
.若在射线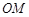 上存在点
上存在点 ,使
,使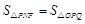 ,请直接写出相应的
,请直接写出相应的 的长.
的长.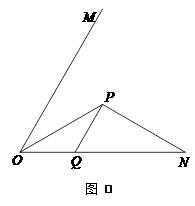
某农场种植一种蔬菜,销售员根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系,观察图象,你能得到关于这种蔬菜的哪些信息?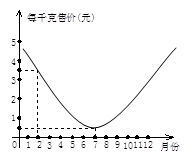
如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外? 
抛物线y=x2- x+a2的顶点在直线y=2上,求a的值.
x+a2的顶点在直线y=2上,求a的值.
当一枚火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用h= -5t2+150t+10表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?
如图,AB是高为1.46米的窗户(窗户朝南),该窗户的遮阳篷呈抛物线形,在图中坐标系内的表达式为y=-x2+0.25,已知该地一年中冬至日正午时刻太阳光线与地面的夹角最小为α,夏至日正午时刻太阳光线与地面的夹角最大为β,且β="73°30′." 若该遮阳篷使冬至日正午时刻太阳光线刚好全部射入室内,夏至日正午时刻太阳光刚好全部不射入室内.求α的度数及遮阳篷顶部到窗户上沿的距离.