如图,AB是高为1.46米的窗户(窗户朝南),该窗户的遮阳篷呈抛物线形,在图中坐标系内的表达式为y=-x2+0.25,已知该地一年中冬至日正午时刻太阳光线与地面的夹角最小为α,夏至日正午时刻太阳光线与地面的夹角最大为β,且β="73°30′." 若该遮阳篷使冬至日正午时刻太阳光线刚好全部射入室内,夏至日正午时刻太阳光刚好全部不射入室内.求α的度数及遮阳篷顶部到窗户上沿的距离.
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的 , 两点,与 轴交于点 ,与 轴交于点 ,点 的坐标是 ,连接 , , .
(1)求反比例函数的解析式;
(2)连接 ,求 的面积.

某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校1600名学生每人都参加且只参加了其中一个社团的活动.校团委从这1600名学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题:

参加本次调查有 名学生,根据调查数据分析,全校约有 名学生参加了音乐社团;请你补全条形统计图.
如图,在 和 中, , , .求证: .

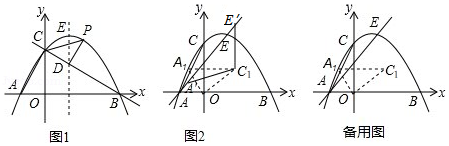
如图1,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 左侧),与 轴交于点 ,抛物线的顶点为点 .
(1)判断 的形状,并说明理由;
(2)经过 , 两点的直线交抛物线的对称轴于点 ,点 为直线 上方抛物线上的一动点,当 的面积最大时, 从点 出发,先沿适当的路径运动到抛物线的对称轴上点 处,再沿垂直于抛物线对称轴的方向运动到 轴上的点 处,最后沿适当的路径运动到点 处停止.当点 的运动路径最短时,求点 的坐标及点 经过的最短路径的长;
(3)如图2,平移抛物线,使抛物线的顶点 在射线 上移动,点 平移后的对应点为点 ,点 的对应点为点 ,将 绕点 顺时针旋转至△ 的位置,点 , 的对应点分别为点 , ,且点 恰好落在 上,连接 , ,△ 是否能为等腰三角形?若能,请求出所有符合条件的点 的坐标;若不能,请说明理由.
在 中, , ,点 是 上一点,连接 ,过点 作 ,在 上取点 ,连接 .延长 至 ,使 ,连接 , ,且 .
(1)若 ,求 的长;
(2)如图1,当点 在 上时,求证: ;
(3)如图2,当点 在 的垂直平分线上时,直接写出 的值.
