如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的 , 两点,与 轴交于点 ,与 轴交于点 ,点 的坐标是 ,连接 , , .
(1)求反比例函数的解析式;
(2)连接 ,求 的面积.

(1)已知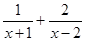 计算结果是
计算结果是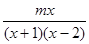 ,求常数m的值;
,求常数m的值;
(2)已知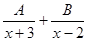 计算结果是
计算结果是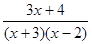 ,求常数A、B的值.
,求常数A、B的值.
如图,△ABC中,O是AC上的任意一点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论.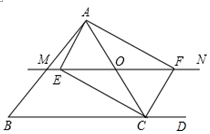
有一道题“先化简,再求值: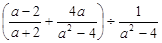 .其中a =-
.其中a =-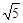 ”马小虎同学做题时把“a = -
”马小虎同学做题时把“a = -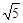 ”错抄成了“a =
”错抄成了“a =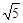 ”,但他的计算结果却与别的同学一致,也是正确的,请你解释这是怎么回事?
”,但他的计算结果却与别的同学一致,也是正确的,请你解释这是怎么回事?
一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外都相同,将球摇匀,从中任意摸出1个球.
(1)能够事先确定摸到的球的颜色吗?
(2)你认为摸到哪种颜色的球的概率最大?
(3)改变袋子中白球、黄球、红球的个数,使摸到这三种颜色的球的概率相等.
观察下列等式: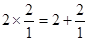 ,
,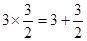 ,
, ,……
,……
(1)按此规律写出第5个等式;
(2)猜想第n个等式,并说明等式成立的理由.