已知函数:
(Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立.
(Ⅱ)当f(x)的定义域为[a+ ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(Ⅲ)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
已知函数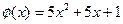
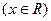 ,函数
,函数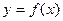 的图象与
的图象与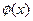 的图象关于点
的图象关于点 中心对称。
中心对称。
(1)求函数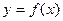 的解析式;
的解析式;
(2)如果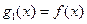 ,
,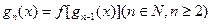 ,试求出使
,试求出使 成立的
成立的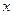 取值范围;
取值范围;
(3)是否存在区间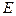 ,使
,使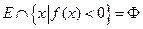 对于区间内的任意实数
对于区间内的任意实数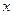 ,只要
,只要 ,且
,且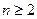 时,都有
时,都有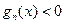 恒成立?
恒成立?
已知三次函数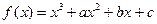 在y轴上的截距是2,且在
在y轴上的截距是2,且在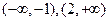 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减.
|
(Ⅰ)求函数f (x)的解析式;
(Ⅱ)若函数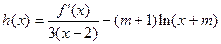 ,求
,求 的单调区间.
的单调区间.
某造船公司年最高造船量是20艘. 已知造船x艘的产值函数R (x)="3700x" + 45x2 – 10x3(单位:万元), 成本函数为C (x) =" 460x" + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) =" f" (x+1) – f (x). 求:(提示:利润 = 产值 – 成本)
(1) 利润函数P(x) 及边际利润函数MP(x);
(2) 年造船量安排多少艘时, 可使公司造船的年利润最大?
(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
甲乙两公司生产同一种新产品,经测算,对于函数 ,
, ,及任意的
,及任意的 ,当甲公司投入
,当甲公司投入 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入 万元作宣传时,甲公司投入的宣传费若小于
万元作宣传时,甲公司投入的宣传费若小于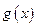 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
(1)请解释 ;
;
(2)甲、乙两公司在均无失败危险的情况下尽可能少地投入宣传费用,问此时各应投入多少宣传费?
(3)若甲、乙分别在上述策略下,为确保无失败的危险,根据对方所投入的宣传费,按最少投入费用原则,投入自己的宣传费:若甲先投入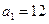 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用 ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为 ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为
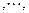 如此得当甲调整宣传费为
如此得当甲调整宣传费为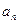 时,乙调整宣传费为
时,乙调整宣传费为 ;试问是否存在
;试问是否存在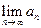 ,
, 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由.