已知函数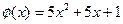
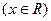 ,函数
,函数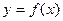 的图象与
的图象与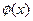 的图象关于点
的图象关于点 中心对称。
中心对称。
(1)求函数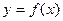 的解析式;
的解析式;
(2)如果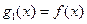 ,
,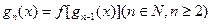 ,试求出使
,试求出使 成立的
成立的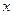 取值范围;
取值范围;
(3)是否存在区间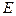 ,使
,使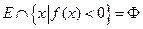 对于区间内的任意实数
对于区间内的任意实数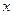 ,只要
,只要 ,且
,且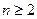 时,都有
时,都有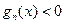 恒成立?
恒成立?
(本小题满分12分)
数列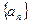 的前n项和记为Sn,已知a1=1,Sn=
的前n项和记为Sn,已知a1=1,Sn=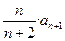 ,(n=1,2,3,……)
,(n=1,2,3,……)
(Ⅰ)求数列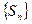 的通项公式;
的通项公式;
(Ⅱ)设Tn=S1+S2+S3+……+Sn,求Tn
给定直线 ,抛物线
,抛物线
(1)当抛物线的焦点在直线 上时,求
上时,求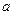 的值
的值
(2)若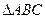 的三个顶点都在(1)所确定的抛物线上,且
的三个顶点都在(1)所确定的抛物线上,且 点的纵坐标为8,
点的纵坐标为8,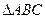 的重心恰是抛物线
的重心恰是抛物线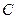 的焦点,求
的焦点,求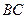 所在直线的方程。
所在直线的方程。
如图,在直三棱柱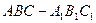 中
中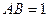 ,
,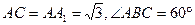
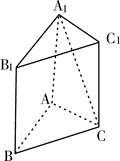
(1)证明: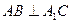
(2)求二面角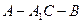 的大小
的大小
某单位为绿化环境,移栽了甲、乙两种大树各2株,设甲,乙两种大树移栽的成活率分别为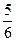 和
和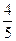 ,求移栽的4株大树中
,求移栽的4株大树中
(1)至少1株成活的概率
(2)两种大树各成活1株的概率
已知函数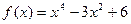
(1)讨论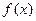 的单调性
的单调性
(2)设点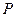 在曲线
在曲线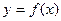 上,若该曲线在点
上,若该曲线在点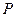 处的切线通过原点,求切线
处的切线通过原点,求切线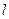 的方程
的方程