已知三次函数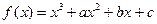 在y轴上的截距是2,且在
在y轴上的截距是2,且在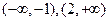 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减.
|
(Ⅰ)求函数f (x)的解析式;
(Ⅱ)若函数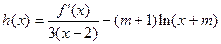 ,求
,求 的单调区间.
的单调区间.如图,在四棱锥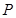 -
- 中,底面
中,底面 是边长为
是边长为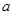 的正方形,
的正方形,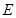 、
、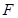 分别为
分别为 、
、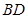 的中点,侧面
的中点,侧面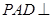 底面
底面 ,且
,且 。
。
(Ⅰ)求证: 平面
平面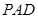 ;
;
(Ⅱ)求证:平面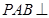 平面
平面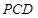 ;
;
(Ⅲ)求三棱锥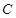 -
-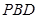 的体积。
的体积。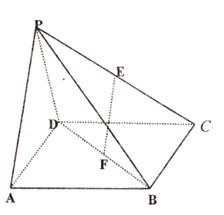
已知点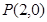 ,及⊙
,及⊙ :
: 。
。
(Ⅰ)当直线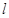 过点
过点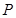 且与圆心
且与圆心 的距离为1时,求直线
的距离为1时,求直线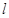 的方程;
的方程;
(Ⅱ)设过点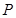 的直线与⊙
的直线与⊙ 交于
交于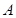 、
、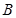 两点,当
两点,当 ,求以线段
,求以线段 为直径的圆的方程。
为直径的圆的方程。
如图,已知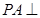 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙ 的直径,
的直径,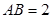 ,
,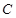 是⊙
是⊙ 上一点,且
上一点,且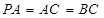 ,
,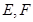 分别为
分别为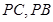 中点。
中点。
(Ⅰ)求证: 平面
平面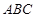 ;
;
(Ⅱ)求证: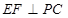 ;
;
(Ⅲ)求三棱锥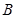 -
-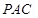 的体积。
的体积。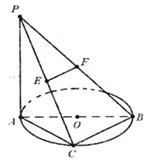
已知圆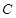 经过两点
经过两点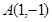 和
和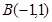 ,且圆心在直线
,且圆心在直线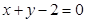 上。
上。
(Ⅰ)求圆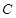 的方程;
的方程;
(Ⅱ)若以圆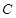 为底面的等边圆锥(轴截面为正三角形),求其内接正方体的棱长。
为底面的等边圆锥(轴截面为正三角形),求其内接正方体的棱长。
已知椭圆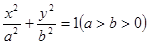 的右焦点为
的右焦点为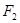 (3,0),离心率为
(3,0),离心率为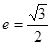 。
。
(1)求椭圆的方程。
(2)设直线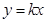 与椭圆相交于A,B两点,M,N分别为线段
与椭圆相交于A,B两点,M,N分别为线段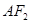 ,
,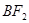 的中点,若坐标原点O在以MN为直径的圆上,求
的中点,若坐标原点O在以MN为直径的圆上,求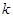 的值。
的值。