.已知椭圆的中心为坐标原点O,焦点在X轴上,椭圆短半轴长为1,动点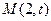
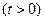 在直线
在直线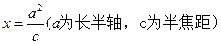 上。
上。
(1)求椭圆的标准方程
(2)求以线段OM为直径且被直线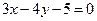 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作直线OM的垂线与以线段OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值。
已知函数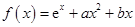 .
.
(Ⅰ)当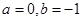 时,求
时,求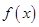 的单调区间;
的单调区间;
(Ⅱ)设函数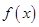 在点
在点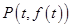
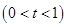 处的切线为
处的切线为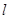 ,直线
,直线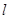 与
与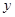 轴相交于点
轴相交于点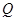 .若点
.若点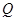 的纵坐标恒小于1,求实数
的纵坐标恒小于1,求实数 的取值范围.
的取值范围.
某工业城市按照“十二五”(2011年至2015年)期间本地区主要污染物排放总量控制要求,进行减排治污.现以降低SO2的年排放量为例,原计划“十二五”期间每年的排放量都比上一年减少0.3万吨,已知该城市2011年SO2的年排放量约为9.3万吨,
(Ⅰ)按原计划,“十二五”期间该城市共排放SO2约多少万吨?
(Ⅱ)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO2的年排放量每年比上一年减少的百分率为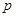 ,为使2020年这一年的SO2年排放量控制在6万吨以内,求
,为使2020年这一年的SO2年排放量控制在6万吨以内,求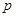 的取值范围.
的取值范围.
(参考数据 ,
, ).
).
某几何体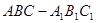 的三视图和直观图如图所示.
的三视图和直观图如图所示.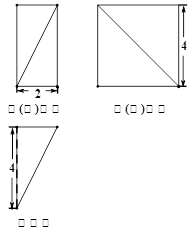
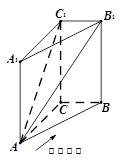
(Ⅰ)求证:平面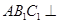 平面
平面 ;
;
(Ⅱ)若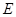 是线段
是线段 上的一点,且满足
上的一点,且满足 ,求
,求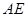 的长.
的长.
已知函数 ,
,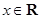 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)试写出一个函数 ,使得
,使得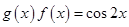 ,并求
,并求 的单调区间.
的单调区间.
(本小题满分12分)
某工厂生产 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
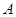 |
7 |
7 |
7.5 |
9 |
9.5 |
 |
6 |
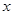 |
8.5 |
8.5 |
 |
由于表格被污损,数据 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(Ⅰ)求表格中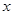 与
与 的值;
的值;
(Ⅱ)若从被检测的5件 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率.