（几何证明4-1）已知⊙O1和⊙O2交于点C和D，⊙O1上的点P处的切线交⊙O2于A、B点，交直线CD于点E，M是⊙O2上的一点，若PE=2，EA=1，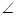
AMB=30o，那么⊙O2的半径为 ；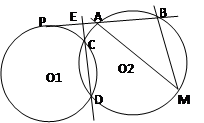
对任意的实数a，b，记max｛a，b｝＝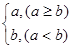
，若
其中奇函数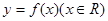
在x=1处有极小值－2，y＝g（x）是正比例函数，函数y＝f（x）（x＞0）与函数y＝g（x）的图象如图所示，则下列关于函数y＝F（x）的说法中，正确的是
| A．y＝F（x）为奇函数 |
| B．y＝F（x）有极大值F（1）且有极小值F（－1） |
| C．y＝F（x）的最小值为－2且最大值为2 |
| D．y＝F（x）在（－3，0）上不是单调函数 |
设ΔABC的三边长分别为a、b、c，ΔABC的面积为S，内切圆半径为r，则r＝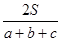
；类比这个结论可知：四面体P－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为R，四面体P－ABC的体积为V，则R＝
A． |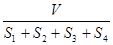
B． |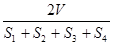
C． |
D． |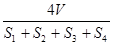
（A）将圆M：x2＋y2＝a（a＞0）的横坐标伸长为原来的2倍，纵坐标缩短为原来的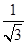
，正好与直线x－y＝1相切，若以原点为极点，x轴非负半轴为极轴建立极坐标系，则圆M的极坐标方程为
（B）关于x的不等式：2－x2＞|x－a|至少有一个负数解，则实数a的取值范围是
把5个不同的小球放入甲、乙、丙3个不同的盒子中，在每个盒子中至少有一个小球的条件下，甲盒子中恰有3个小球的概率为
已知O（0，0），A（1，0），B（1，1），C（0，1），向正方形OABC内投一个点P，点P落在函数y＝xα（α＞0）与y＝x所围封闭图形内的概率为
，则实数α的取值是