(1)经计算发现: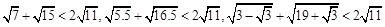 ,
,
试写出一个使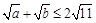 成立的正实数
成立的正实数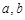 满足的条件,并给出证明;
满足的条件,并给出证明;
(2)若不等式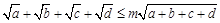 对任意的正实数
对任意的正实数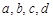 恒成立,
恒成立,
求实数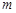 的取值范围.
的取值范围.
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.
(1)求P(A),P(B),P(AB);
(2)当已知蓝色骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
盒子里装有16只球,其中6只是玻璃球,另外10只是木质球.而玻璃球中有2只是红色的,4只是蓝色的;木质球中有3只是红色的,7只是蓝色的,现从中任取一只球,如果已知取到的是蓝色的球,求这个球是玻璃球的概率.
某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现有一个20岁的动物,求它能活到25岁的概率.
在数列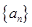 中,
中,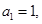 且对任意的
且对任意的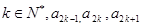 成等比数列,其公比为
成等比数列,其公比为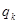 ,
,
(1)若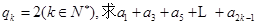 ;
;
(2)若对任意的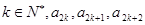 成等差数列,其公差为
成等差数列,其公差为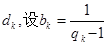 .
.
①求证: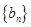 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若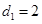 ,试求数列
,试求数列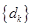 的前
的前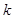 项和
项和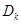 .
.