设 、
、 分别为椭圆
分别为椭圆 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ) 若椭圆C上的点 到
到 、
、 两点的距离之和等于4, 写出椭圆C的方程和离心率.;
两点的距离之和等于4, 写出椭圆C的方程和离心率.;
(Ⅱ) 若M、N是椭圆C上关于原点对称的两点,点P是椭圆上除M、N外的任意一点, 当直线PM、PN的斜率都存在, 并记为 、
、 时, 求证:
时, 求证:  ·
· 为定值.
为定值.
已知椭圆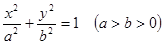 的离心率为
的离心率为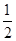 ,长轴长为4,
,长轴长为4, 为左顶点,过左焦点
为左顶点,过左焦点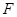 的直线与椭圆交于
的直线与椭圆交于 两点,直线
两点,直线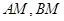 与
与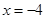 分别交于
分别交于 两点,(
两点,( 两点不重合).
两点不重合).
(1)求椭圆的标准方程;
(2)当直线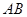 与
与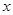 轴垂直时,求证:
轴垂直时,求证:
 (3) 当直线
(3) 当直线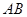 的斜率为
的斜率为 时,(2)的结论是否还成立,若成立,请证明;若不成立,说明理由.
时,(2)的结论是否还成立,若成立,请证明;若不成立,说明理由.
某市旅游部门开发一种旅游纪念品,每件产品的成本是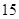 元,销售价是
元,销售价是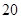 元,月平均销售1000件.通过改进工艺,产品的成本不变,质量和技术的含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
元,月平均销售1000件.通过改进工艺,产品的成本不变,质量和技术的含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为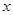
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 .设改进工艺后,旅游部门销售该纪念品的月平均利润是
.设改进工艺后,旅游部门销售该纪念品的月平均利润是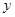 (元).
(元).
(1)当销售价提高的百分率为0.1时,月利润是多少?
(2)写出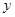 与
与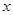 的函数关系式;
的函数关系式;
(3)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
已知函数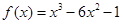 .
.
(1)求函数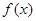 的单调区间与极值;
的单调区间与极值;
(2)设 ,且
,且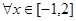 ,
,
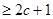 恒成立,求
恒成立,求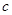 的取值范围.
的取值范围.
抛物线顶点在原点,焦点在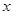 轴上,且过点
轴上,且过点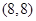 ,焦点为
,焦点为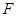 ;
;
(1)求抛物线的焦点坐标和标准方程:
(2)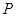 是抛物线上一动点,
是抛物线上一动点,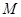 是
是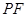 的中点,求
的中点,求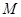 的轨迹方程.
的轨迹方程.
已知函数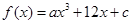 在
在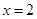 处有极大值8,求实数
处有极大值8,求实数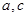 的值.
的值.