已知,如图,A,B分别在x轴和y轴上,且OA=2OB,直线y1=kx+b经过A点与抛物线y2=-x2+2x+3交于B,C两点,
(1)试求k,b的值及C点坐标;
(2)x取何值时y1,y2均随x的增大而增大;
(3)x取何值时y1>y2.
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.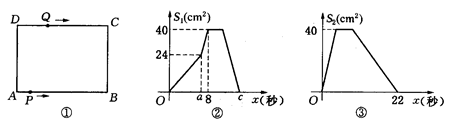
(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
如图1,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.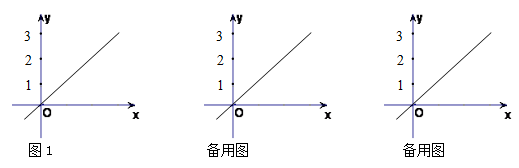
在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.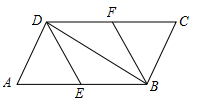
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
已知,如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.四边形ABCD是平行四边形吗?请说明理由.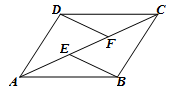
为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.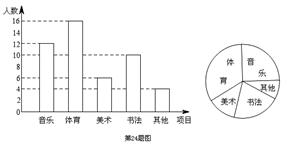
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数