在△ABC中，角A、B、C的对边分别为a、b、c，向量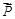
=（sinA,b+c），
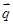=（a－c,sinC－sinB）,满足
=
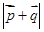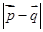（Ⅰ）求角B的大小；（Ⅱ）设
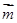=（sin（C+
）,
）, 
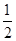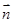=（2k,cos2A） （k>1）, 
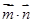有最大值为3，求k的值.
如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数
，
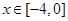时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧．
（1）试确定A，
和
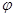的值；
（2）现要在右侧的半圆中修建一条步行道CDO（单位：米），在点C与半圆弧上的一点D之间设计为直线段（造价为2万元/米），从D到点O之间设计为沿半圆弧的弧形（造价为1万元/米）．设
（弧度），试用
来表示修建步行道的造价预算，并求造价预算的最大值？（注：只考虑步行道的长度，不考虑步行道的宽度）
已知函数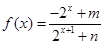
，（其中
、
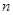为参数）
（1）当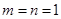
时，证明：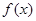
不是奇函数；
（2）如果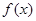是奇函数，求实数、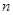的值；
（3）已知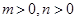
，在（2）的条件下,求不等式
的解集．
已知函数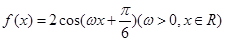
的最小正周期为
．
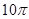（1）求函数
的对称轴方程；
（2）设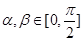
，
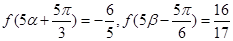，求
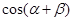的值．
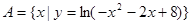设集合
，集合
，集合C为不等式
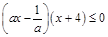的解集．
（1）求
；
（2）若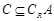
，求a的取值范围．
甲、乙两人玩转盘游戏，该游戏规则是这样的：一个质地均匀的标有12等分数字格的转盘（如图），甲、乙两人各转转盘一次，转盘停止时指针所指的数字为该人的得分．（假设指针不能指向分界线）现甲先转，乙后转，求下列事件发生的概率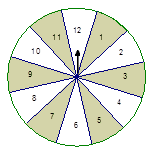
（1）甲得分超过7分的概率．
（2）甲得7分，且乙得10分的概率
（3）甲得5分且获胜的概率．