（文科）某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
[230，235) |
8 |
0.16 |
| 第二组 |
[235，240) |
① |
0.24 |
| 第三组 |
[240，245) |
15 |
② |
| 第四组 |
[245，250) |
10 |
0.20 |
| 第五组 |
[250，255] |
5 |
0.10 |
| 合 计 |
50 |
1.00 |
（1）写出表中①②位置的数据；
（2）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数；
（3）在（2）的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率．
已知命题P：“
，都有不等式
成立”，命题Q：“关于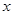
的方程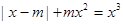
只有一个实数根”
（Ⅰ）若命题P是真命题，求实数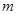
的取值集合B；
（Ⅱ）若命题“P且Q”为假，命题“P或Q”为真，求实数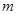的取值范围．
设集合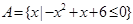
，关于x的不等式
的解集为B（其中a＜0）．
（Ⅰ）求集合B；
（Ⅱ）设p：x∈A，q：x∈B，且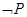
是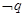
的必要不充分条件，求实数
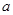的取值范围．
某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段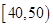
，
…
后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：
（1）求第四小组的频率，并补全频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“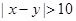
”的概率．
已知函数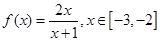
（1）求证：
在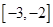
上是增函数；
（2）求的最大值和最小值．
（本小题12分）下表是关于某设备的使用年限（年）和所需要的维修费用y （万元）的几组统计数据：
 |
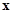2 |
3 |
4 |
5 |
6 |
 |
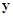2．2 |
3．8 |
5．5 |
6．5 |
7．0 |
（1）请在给出的坐标系中画出上表数据的散点图；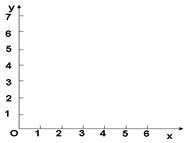
（2）请根据散点图，判断y与x之间是否有较强线性相关性，若有求线性回归直线方程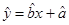
；
（3）估计使用年限为10年时，维修费用为多少？（参考数值：
）
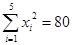（参考公式：
；
；）